Intervals Enhance the Intelligent Experience
Forecasting sales is a hard problem for businesses to solve, especially given that the focus on hitting an exact number is often top of mind for decision-makers. However, it is difficult to predict an exact number, even when organizations have access to high-quality data and sophisticated predictive models. Business processes are often characterized by uncertainty, so forecasts should account for this inherent uncertainty. Interval-based estimation allows a user to generate a forecasted value, called a point estimate, with a range of plausible values around it. This range of plausible values can be designed so that they capture the true value a high percentage of the time, providing flexible, yet accurate predictions of a given quantity.
What is Uncertainty and How Do We Account for It?
Forecasting with a single number can be a very hard problem – in fact, in statistics, it’s often very difficult to accurately predict a single number in any context (not just forecasting). Consider the problem of estimating the winner of an election. It would be very difficult to accurately predict the precise percentage of votes a candidate might earn; however, it typically suffices to know whether that prediction is greater or less than 50 percent. This highlights the need for interval forecasts – a point estimate with a range of plausible values called a confidence interval (CI).
Additionally, without understanding the variability inherent in the quantity to be predicted, a forecast’s accuracy may be hard to assess, highlighting the key question: What differentiates a good forecast from a bad one? In a good forecast, the actual value should be pretty close to the value that is forecasted, meaning that it should be within the forecasted confidence interval (of reasonable width). A bad forecast may fit into one of two categories: either the actuals do not fall within the width of the CI, or the CI is too wide to be useful in practice.
For instance, here’s an example of a couple of good forecasts:
- Higher-Ed Enrollment Predictions: A university forecasts the number of incoming students to be 22,500 +/- 500. The actual value is 22,300, but when we consider the range of plausible values given the variability in the data, being off by 200 is quite small relative to the uncertainty in the data.
- Revenue Forecasts: A sales forecast estimates that a company will sell 5 +/- 1.5 million dollars in the next calendar year, but in reality, the company sells 6 million the next year.
Because both values fall with (relatively narrow) confidence intervals, they represent good forecasts. In a similar vein, a bad forecast may not be apparent at first glance.
Here are a couple of problematic scenarios:
- Overestimating the “Worst Case” Scenario: A high-dollar, low-transaction real estate firm forecasts the number of sales they will make in a given year at 150 +/- 10 sales. However, they overestimate by 20 sales, making only 130 sales throughout the year. This means that they did not even make their “worst-case” scenario of 140 sales, meaning the forecast gave bad advice.
- Polling CI: A polling company estimates the proportion of voters that are likely to support a ballot measure is 45 +/- 30%. This interval means that any value between 15% and 75% is plausible, so even if that interval captures the true value, it may not be useful.
Forecast quality is a function of the quality and specificity of the data used and the methods employed. Typically, improvement of a forecast should be focused on accomplishing one of the following goals:
- Narrow the CI: Without reducing the accuracy of the interval, provide a narrower interval around the forecasted quantity.
- Increase Capture of Actuals: Capture a higher percentage of actual observed values given the width of the CI.
Fantasy Football Forecasting: An Example
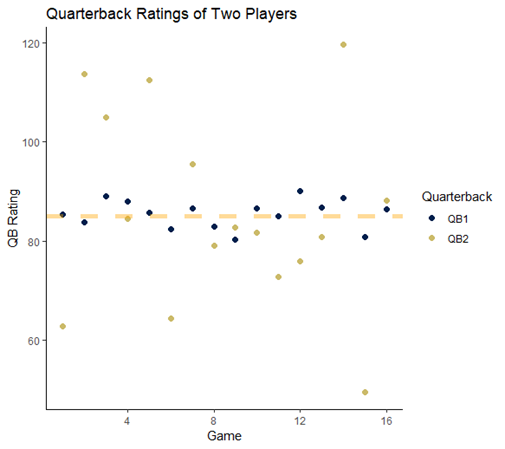
Think of it this way – many people play fantasy football during the NFL season. Consider two quarterbacks. Over the course of the season, they have the same average quarterback rating, which tracks how well each quarterback plays during a given game. QB1 is very consistent – this player’s quarterback rating is almost always between 80 and 90. On the other hand, QB2 experiences wildly disparate swings in play – one week he plays very well, with QB ratings over 120, and the next, he might play very poorly. The difference between the two players is that QB1 has low variability and QB2 has very high variability.
Figure 1: QB ratings for two quarterbacks shows a narrow, consistent spread for QB1 and a wides pread for QB2.
If you had to make a choice as to which quarterback is going to have a better performance in the next week, you might be tempted to pick QB2 since he has the highest performance peaks. However, QB1 is probably the safer bet. This is the same problem faced by organizations when trying to forecast important KPIs – some are highly variable and others are not.
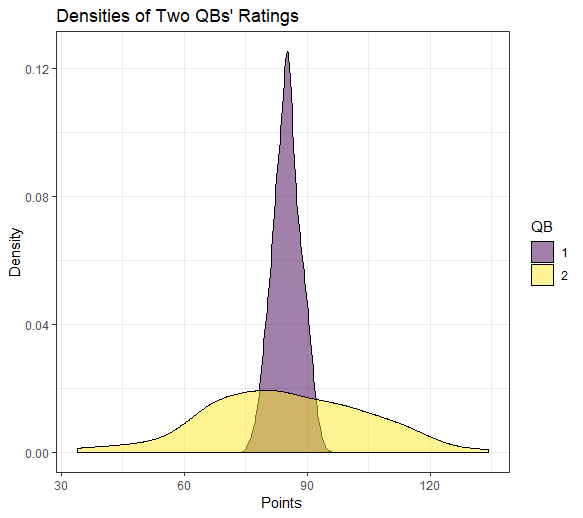
Figure 2: The distributions of QB ratings for both quarterbacks shows the differences in expected ranges of values, despite having the same mean.
Using Interval Estimates
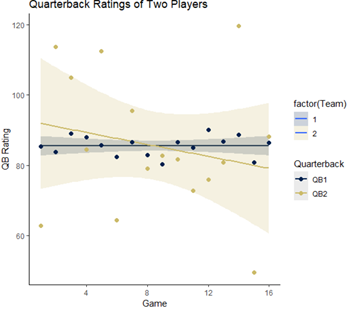
These examples illustrate the need for interval-based forecasts or at least a method that takes into account the variability in the data and the scale of the quantity being predicted. Intervals allow organizations to assess both a worst-case and best-case scenario based on the amount and quality of the data, establishing a range of plausible values for each forecast. Returning to our two-quarterback quandary, we might be able to better inform our question of which one to pick by calculating a confidence interval for each player’s predicted quarterback rating. Looking at the plot below, we can see that the shaded confidence band for QB2 indicates that his next quarterback rating could plausibly fall between 60 and 100 – a wide interval indeed! QB1 is a much safer bet with a confidence interval between 83 and 88.
Figure 3: Confidence intervals around each QB’s observed ratings indicate wide spread for QB2 and narrow interval for QB2.
In some cases, it may make sense to create intentionally conservative or aggressive forecasts. One way to do this would be to generate a forecast using a standard statistical method, perhaps something like the Holt-Winters exponential smoothing model used in Salesforce Analytics. Rather than using the predicted mean value, an intentionally aggressive forecast might target the upper confidence limit, or an intentionally conservative forecast might target the 3. This idea might come into play if over or under-forecasting has the potential to create more serious organizational problems.
Confidence intervals (sometimes called prediction intervals when used in forecasting) tell us, for a certain level of confidence, a reasonable range of values in which the parameter of interest should fall. For QB1, we would expect that 95% of the time, his QB rating would fall between 82 and 88, whereas, for QB2, we would expect that range to be between 65 and 100. Practically, this means that throughout the season, we would expect each quarterback’s QB rating to be within these limits, with one observation outside the CI occurring roughly once in a 20-game stretch, based on a 5% significance level.
How Do Intervals Work in Opportunity-Based Forecasting?
We know that intervals are helpful for identifying best and worst-case scenarios, as well as quantifying the variability in our estimated forecast. However, we should think a bit more about how these might be implemented into a smart, data-driven forecast that can be used in a CRM environment. If you’ve read Atrium’s forecasting whitepaper or my blog on different forecasting methods, you’ve heard of two key approaches for generating CRM forecasts: Top-down and bottom-up forecasts.
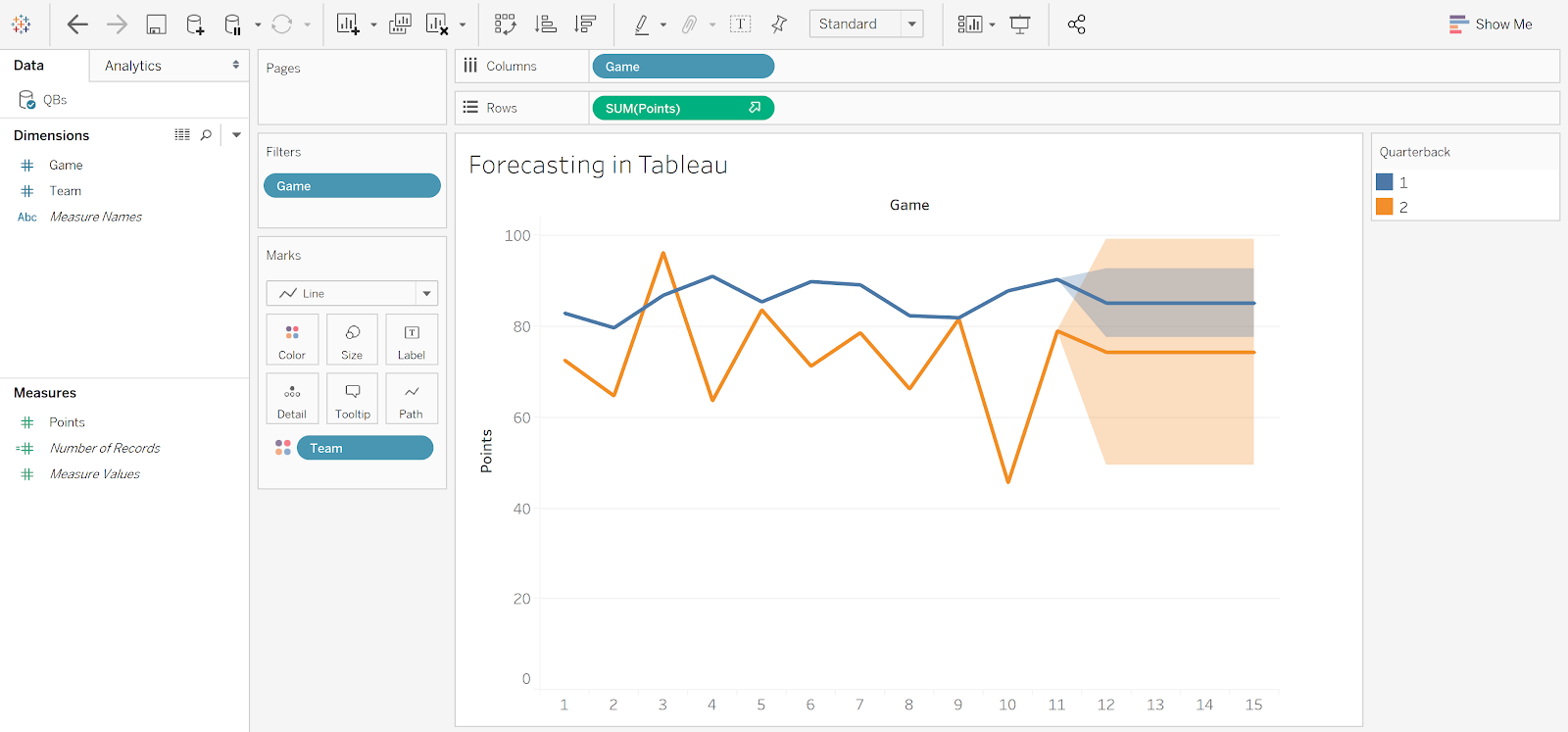
In a top-down framework, data are aggregated, so a forecast often looks like a predicted line or value. Most methods that are used in this setting have associated confidence intervals. In Salesforce Analytics’ timeseries function, 95% prediction intervals can be added at the touch of a button. Similarly, Tableau allows for intervals to be added to their suite of 7 different forecasting methods.
Figure 4: Forecasting final 4 games for quarterbacks in Tableau allows for different confidence intervals in forecasted spreads based on 7 different forecasting methods, including exponential smoothing (pictured here).
In the bottom-up approach, sales opportunities or leads are first scored using a logistic regression model, and then that score is used to calculate an expected deal value. Rather than simply using the predicted conversion score, we can instead use a confidence interval for each score to generate a range of plausible expected deal values. These can then be rolled up by team, region, manager, or a different meaningful grouping to generate an overall forecast interval.
Much like point-based opportunity forecasting, interval-based opportunity forecasting can be implemented in a downstream dashboard in Analytics, Tableau, or whatever consumption layer you are using. Automated actions can be enabled based on the forecasted value, or, perhaps more usefully, on the upper/lower bounds of the generated prediction intervals.
Final Thoughts
Enabling and improving the intelligent CRM experience is all about finding better ways to make data-driven decisions. Part of that improvement comes from making improvements to the data themselves, based on the identification of data gaps or via opportunities to make data practices better or more consistent. Additionally, utilizing better statistical and machine-learning tools can make results easier to interpret and decisions easier to make. By considering the effect of uncertainty and generating interval-based estimates, forecasts can consider more than just a single target. An entire range of plausible values can be considered when making decisions, from the ‘best-case’ to the ‘worst-case’.